树的基础知识
树的定义:
- 树包含n(n ≥≥ 0 )个节点,n = 0时称为空树。
- 在树的结构关系中,有且仅有一个节点没有前趋节点,这个节点称为树的根节点。
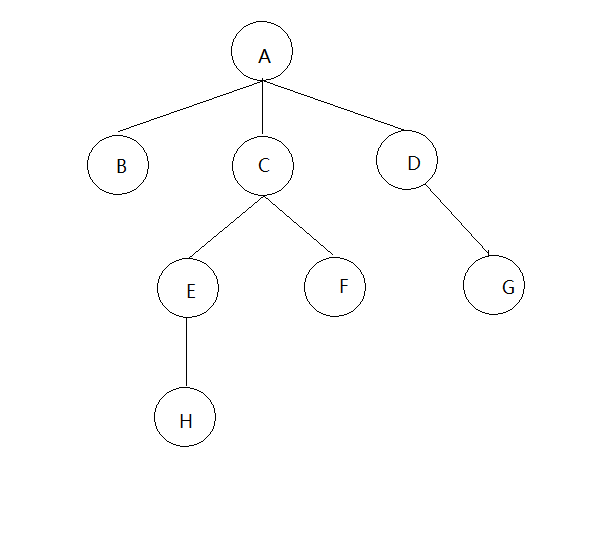
- 除根节点外,树中其他的节点有且仅有一个前趋节点,但可以有很多后继节点。如图,A为根节点。
树的基本术语:
- 结点的度:每个节点具有的子树的个数(后继节点的个数)称为该节点的度;A的度为3,B的度为0。(节点的度 = 节点的孩子节点 = 节点的后继节点)
- 树的度:树中所有节点的度的最大值;图中树的度为3。(树的度 取 所有节点度的最大值)
- 分枝节点:度大于0的节点。(有分枝【孩子节点,后继节点,度】的节点)
- 叶子节点:度为0的节点;如B、H、F、G。
- 孩子节点:一个节点的后继称为该节点的孩子节点;B为A的孩子节点。
- 父亲节点:一个节点的前趋称为该节点的父亲节点;A为B的父亲节点。
- 子孙节点:一个节点的所有子树中的节点称为该节点的子孙节点。(例如C的子孙节点是E、F、H)
- 祖先节点:从树根节点到达某个节点的路径上所通过的所有节点称为该节点的祖先节点。(H的祖先节点是E、C、A)
- 兄弟节点:具有相同父亲节点的节点;B、C、D为兄弟节点。
- 节点的层数:从上到下,根为第一层。(H在第四层)
- 树的深度:树中节点的最大层数称为树的深度或高度;图中树深为4。
二叉树的定义:二叉树是指树的度为2的有序树。左边的为左子树,右边的为右子树。
二叉树常被用于实现二叉查找树和二叉堆。
二叉树的性质:
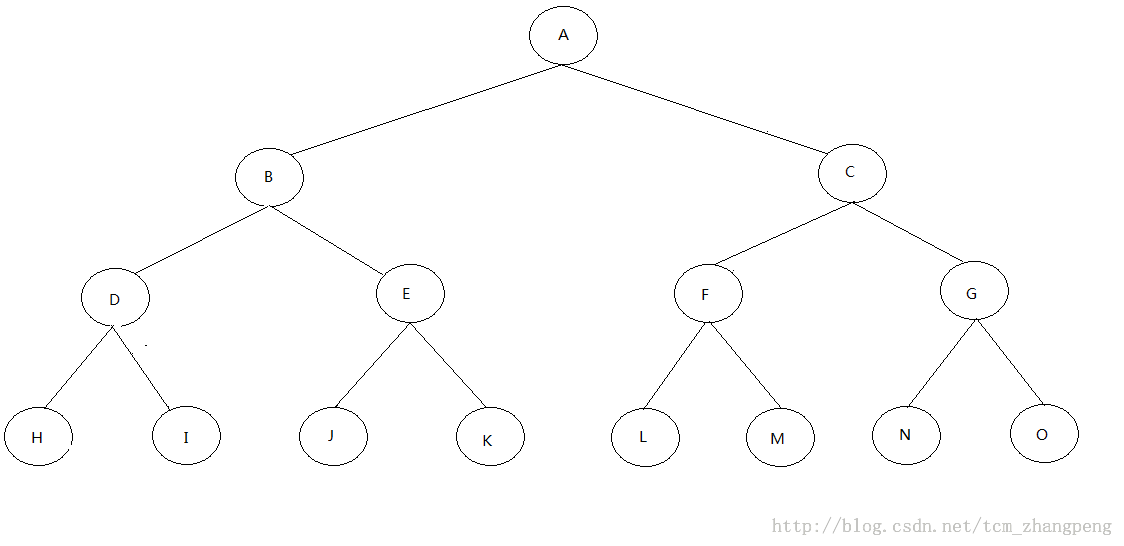
- 二叉树上叶子节点数等于度为2的节点数加1。(上面树的度[子孙节点]为2的几点有7个,叶子节点有8个)
- 二叉树上第i层上最多有
个节点(i ≥ 1)。(上面的树第2层有 2个节点)
- 深度为h的二叉树最多有
个节点。
二叉树的遍历:
- 二叉树的先序遍历:先遍历根节点,再遍历左子树,再遍历右子树。(第一个是根节点,最后一个所有树的最后一个节点)
- 二叉树的中序遍历:先遍历左子树,再遍历根节点,再遍历右子树。(第一个是最后一层的第一个节点,最后一个最后一层的最后一个节点)
- 二叉树的后序遍历:先便利左子树,再遍历右子树,再遍历根节点。(第一个是最后一层的第一个节点,最后一个根节点)
- 二叉树的层次遍历:从上到下逐层遍历,根节点为第一层。
先序遍历为:A BDH I E JK – CFL M G NO
中序遍历为:HDIBJEK A LFMCNGO
后序遍历为:HID JKE B – LMF NOG C A
层次遍历为:A BC DEFG HIJKLMNO
二叉树的重建
- 已知二叉树的先序遍历和中序遍历,可重建二叉树;
- 已知二叉树的后序遍历和中序遍历,可重建二叉树;
- 已知二叉树的先序遍历和后序遍历不能重建二叉树,因为无法确定左子树和右子树,所以重建所得二叉树不唯一。
根据 前序遍历结果 和 中序遍历结果 重建二叉树 递归解法
package ins.platform.web.dd.web.action; /** * 重建二叉树 递归解法 * * @author DELL * */ public class RebuildBinTree { // 定义节点类 public static class Node { int left; // 左子树位置 int right; // 右子树位置 char value; // 节点值 public Node(int left, int right, char value) { this.left = left; this.right = right; this.value = value; } public void setLeft(int left) { this.left = left; } public void setRight(int right) { this.right = right; } } /** * 重建二叉树 * * @param preOrder * 前序遍历结果 * @param inOrder * 中序遍历结果 * @param tree * 重建的树 * @param root * 当前重建树的根节点位置 */ public static void rebuild(String preOrder, String inOrder, Node[] tree, int root) { int nTreeLen = preOrder.length(); // 检查边界条件 if (preOrder.length() == 0 || inOrder.length() == 0) return; // 获取当前遍历的第一个节点 Node temp = new Node(-1, -1, preOrder.charAt(0)); // 如果节点为空,把当前节点复制到根节点 if (tree[root] == null) { tree[root] = temp; } // 如果当前树的长度为1,那么已经是最后一个节点 if (nTreeLen == 1) { return; } // 寻找左子树的结尾 int i = 0; while (inOrder.charAt(i) != temp.value && i < nTreeLen) { i++; } // System.out.println(i); // 重建左子树 int index = root; if (i > 0) { tree[index].setLeft(++root); Node left = new Node(-1, -1, preOrder.charAt(1)); tree[root] = left; // System.out.println(preOrder.substring(1,i+1)+" "+i); rebuild(preOrder.substring(1, i + 1), inOrder.substring(0, i), tree, root); } // 重建右子树 if (nTreeLen - i - 1 > 0) { tree[index].setRight(root + i); Node right = new Node(-1, -1, preOrder.charAt(i + 1)); tree[root + i] = right; rebuild(preOrder.substring(i + 1, nTreeLen), inOrder.substring(i + 1, nTreeLen), tree, root + i); } } public static void main(String[] args) { String preOrder = "ABDHIEJKCFLMGNO";//abdcef //ABDHIEJKCFLMGNO String inOrder = "HDIBJEKALFMCNGO";//dbaecf //HDIBJEKALFMCNGO Node[] tree = new Node[preOrder.length()]; rebuild(preOrder, inOrder, tree, 0); System.out.println("重建的树为:"); for (int i = 0; i < tree.length; i++) { String left, right; if (tree[i].left != -1) left = String.valueOf(tree[tree[i].left].value); else left = null; if (tree[i].right != -1) right = String.valueOf(tree[tree[i].right].value); else right = null; System.out.println(tree[i].value + " 左子树:" + left + " 右子树:" + right); } } }
输出结果为:
重建的树为: A 左子树:B 右子树:C B 左子树:D 右子树:E D 左子树:H 右子树:I H 左子树:null 右子树:null I 左子树:null 右子树:null E 左子树:J 右子树:K J 左子树:null 右子树:null K 左子树:null 右子树:null C 左子树:F 右子树:G F 左子树:L 右子树:M L 左子树:null 右子树:null M 左子树:null 右子树:null G 左子树:N 右子树:O N 左子树:null 右子树:null O 左子树:null 右子树:null
主要思路是 先序遍历的第一个节点是根节点、在中序遍历中可以根据根节点找到左子树,循环找左子树,直到找到最后一层的第一个节点