梯度是什么

梯度: 是一个向量, 导数+变化最快的方向(学习的前进方向)
回顾机器学习
收集数据(x),构建机器学习(f),得到(f(x,w)=Y_{predict})

在有(x)和(y)的情况下(测试数据集),我们是没有办法找到(w)的,那么我们就要有一个损失函数,把寻找(w)的过程转换为寻找损失函数最小值的过程.

判断模型好坏的方法

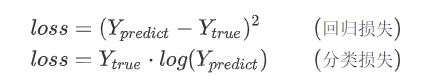
目标: 通过调整(学习)参数(w),尽可能的降低(loss),那么我们该如何调整(w)呢?

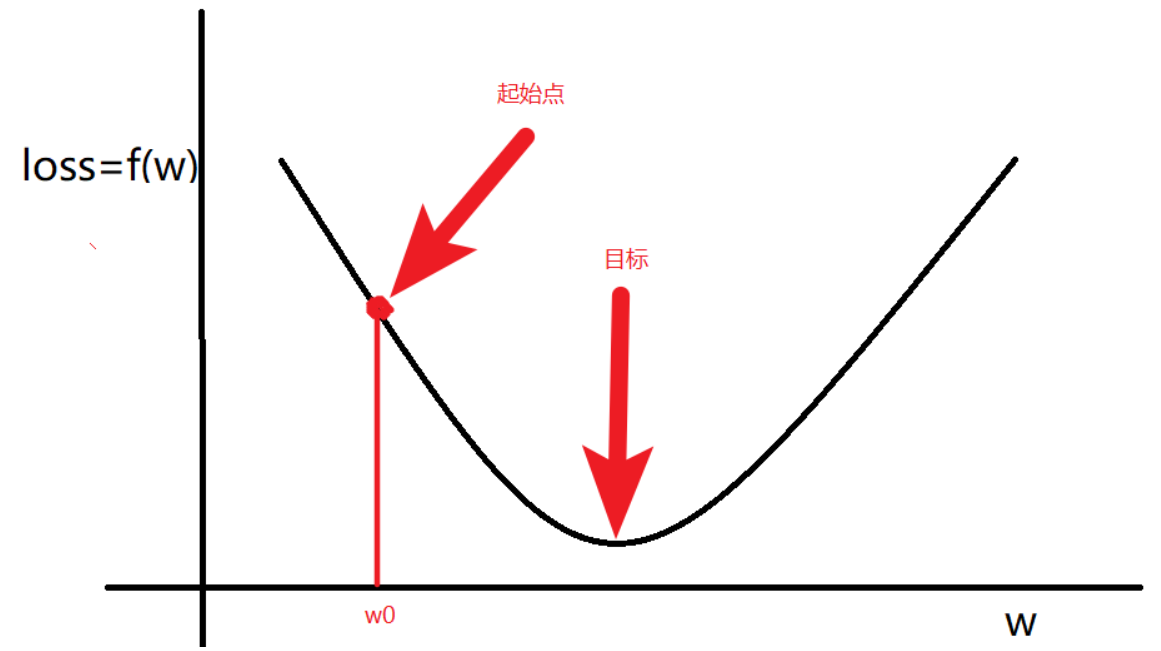
如上图,一开始我们会随机选择一个(w_0)作为起始点,然后目标(w)如图所示,让(loss=f(w))取到最小值

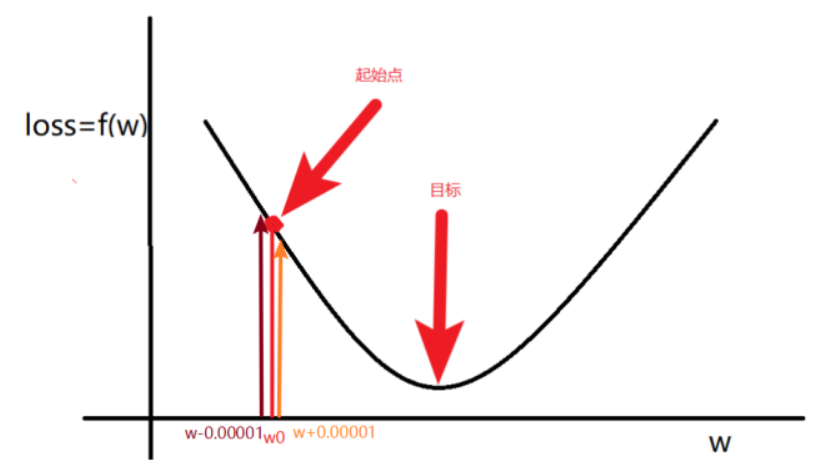
可以取一个很小的值来制造一个小区间,来进行导数的求解,这里取(0.00001).
下面是更新(w)的方法:

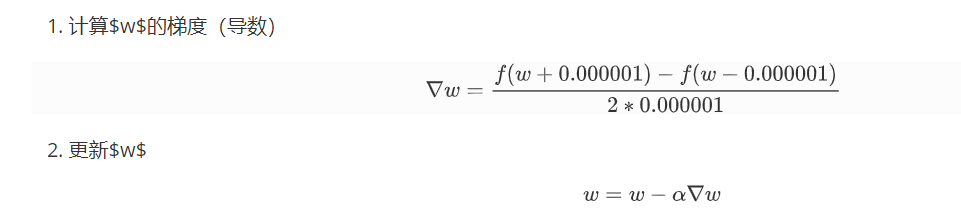
其中:
(1) 如果(▽w<0),意味着(w)将增大
(1) 如果(▽w>0),意味着(w)将减小

总结: 梯度就是多元函数参数的变化趋势(参数的学习方向).

偏导的计算

常见的导数计算

如何求解(f(x)=(1+e^{-x})^{-1})
使用链式求导法则
(f(a)=a^{-1}) ==> (-a^{-2})
(a(b)=1+b) ==> (1)
(b(c)=e^c) ==> (e^c)
(c(x)=-x) ==> (-1)
最后(f(a)*a(b)*b(c)*c(x)=a^{-2}e^{-x}=(1+e^{-x})^{-2}e^{-x}))

多元函数求偏导

一元函数,即有一个自变量.类似(f(x))
多元函数,即有多个自变量,类似(f(x,y,z)),有三个自变量.
多元函数求偏导过程中: 对某一个自变量求导,把其他自变量当做常量.

练习: 已知(J(a,b,c)=3(a+bc)),令(u=a+v),(v=bc),求(a,b,c)各自的偏导数

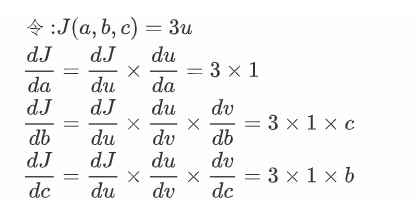
反向传播算法

计算图和反向传播

计算图: 通过图的方式来描述函数的图形
在上面的练习中,J(a,b,c)=3(a+bc),令u=a+v,v=bc,把它绘制成计算图可以表示为

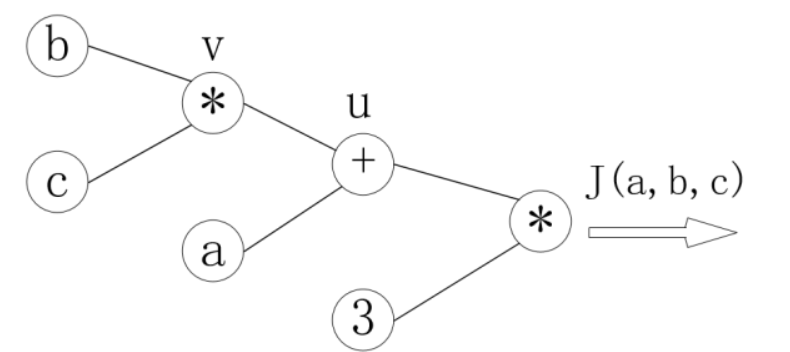
绘制成计算图之后,可以清楚的看到向前计算的过程.

之后,对每个节点求偏导,有

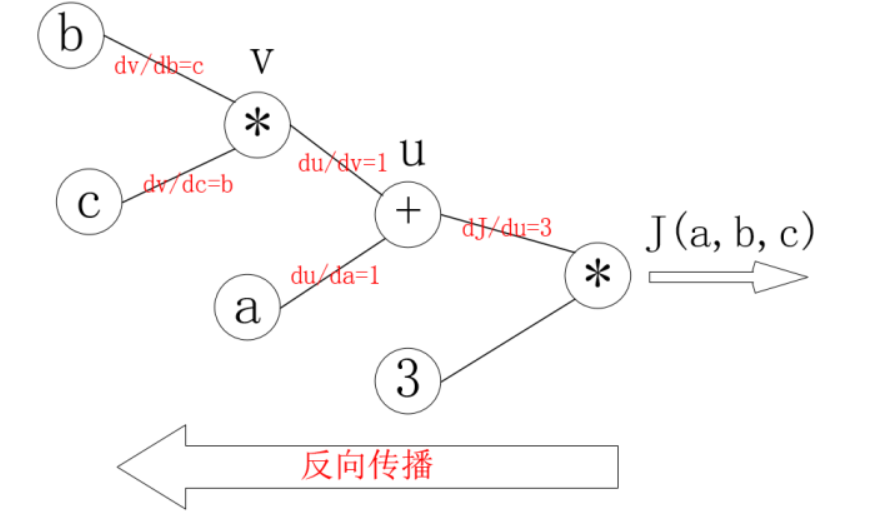
那么反向传播的过程就是一个上图的从右往左的过程,自变量(a,b,c)各自的偏导就是连线上的梯度的乘积.

神经网络中的反向传播

神经网络的示意图

(w_1,w_2,….w_n)表示网络第n层权重
(w_n[i,j])表示第n层第i个神经元，连接到第n+1层第j个神经元的权重。

神经网络的计算图

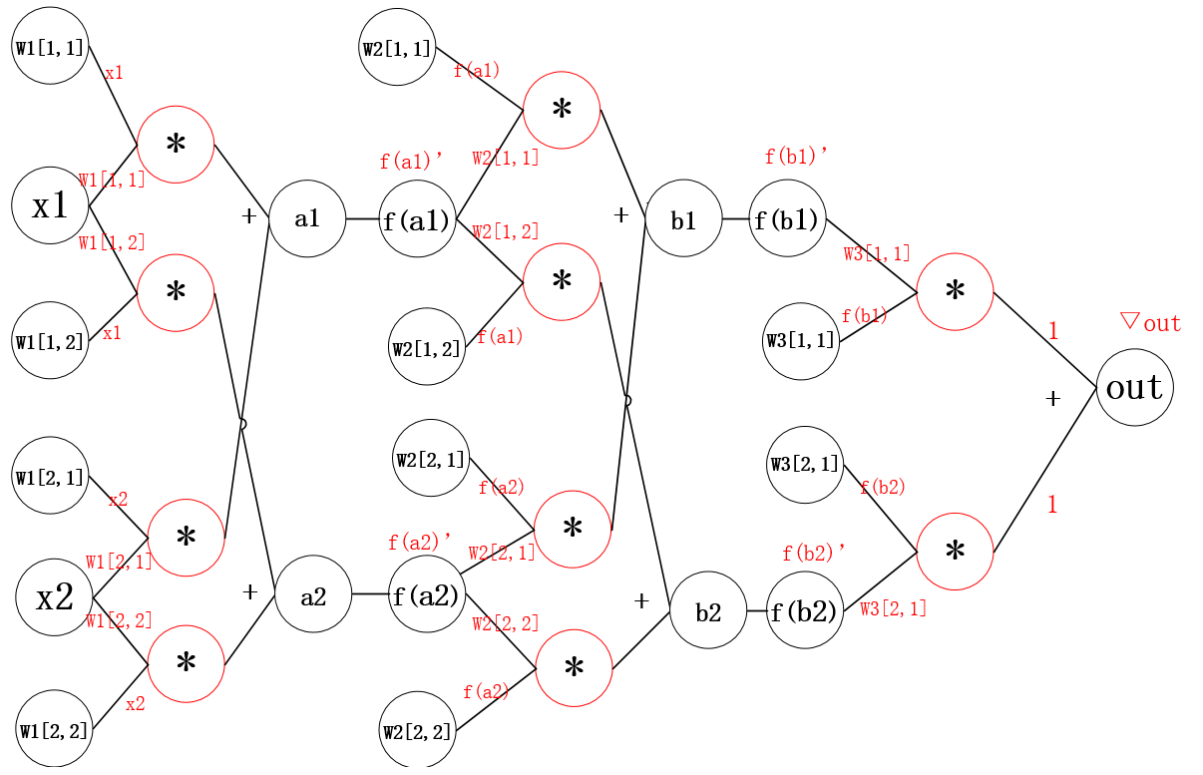
反向传播就是从后往前计算每一层的梯度,直到计算到第一层.

小结

1. 如何理解梯度? 
梯度是一个向量: 导数+变化率最快的方向

2. 损失函数的作用是什么? 
作用: 帮助寻找合适的权重w
对于 y=f(wx+b), y和x是已知的,但是w是不知道的.
所以现在需要一个损失函数,把寻找合适的w转化为寻找损失函数最小值的过程.

3. 什么是计算图?计算图如何求偏导? 
计算图: 以图的形式表示函数的图形
画出J(a,b,c)=3(a+bc),令u=a+bc,v=bc 的计算图
从右往左依次把连线上的偏导进行相乘.

4. 什么是反向传播? 
反向传播就是计算图从右往左的计算过程. 
从右往左其实就是一个求自变量偏导的一个过程,求偏导就是为了得到自变量的梯度,然后不断去更新梯度,去逼近结果. 

5. BP算法大理解！
首先清楚什么是计算图
正向传播，就是从第一层输入，然后一次推到最后一层
权重一开始的输入可以是随机值，没有关系的。 有一个叫做损失函数的东西，可以给出最终结果的梯度。
那么就开始反向传播了，也就是输入的值是最终结果的梯度，然后如何得到之前每一层的梯度呢？ 就是链式求导法则，这样可以一层一层的向前求出每一层每一个节点的梯度。

最后一个问题，求梯度干什么？
就是为了更新w的值，w=w-lr*grad , b=b-lr*grad